Co-ordinate Rule Validation

Wynwood Walls, Miami

A rule looks like this:
  A NE B
This means this means point A is located northeast of point B.
  A SW C
means that point A is southwest of C.
Given a list of rules, check if the sum of the rules validate. For example:

  A N B 

  B NE C

  C N A

does not validate, since A cannot be both north and south of C.

  A NW B

  A N B

is considered valid.

Understanding the problem

Each sentence is a rule that specifies the location of the first point relative to the second point. As we process these rules we need to validate that all these rules are correct.

Solving it

We can easily assume that the logical approach to be some sort of directed graph. Each node in the graph could represent the point and also specify the direction to a node it points to. As we start to populate this graph, it become evident that this can quickly turn into a cumbersome solution. 

• Each new node requires the validation of the entire graph to ensure the addition did not invalidate another relationship. 
• Alternatively we can propagate all directional relationship upon each new node addition, but this will increase insert time considerably in large graphs

We can certainly pivot this graph solution into another data structure that stores the directional relationship like a map of maps. But this too will prove to have the same complications of updating and validation that a directed graph has.

Using a grid

Rather than preserving the directional relationship  (North, North-West), we can instead assign each point a co-ordinate.

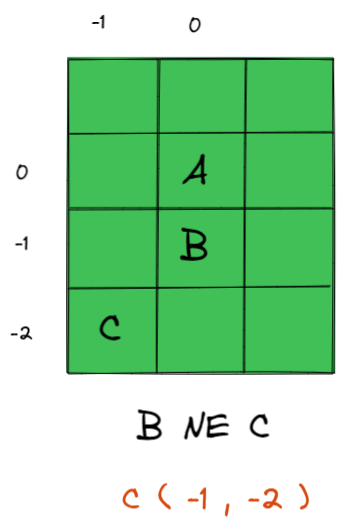
Lets start with the first rule - A N B. We haven't seen either point before therefore we can start by assigning the starting co-ordinates of (0,0) to A. Since A lies north of B (and B lies south of A), we can calculate the co-ordinate of B relative to A by subtracting 1 from the Y co-ordinate. 

B is therefore assigned the co-ordinate of (0,-1)

For the next rule B NE C, we have seen B before, however we haven't seen C. We can therefore generate the co-ordinate for C relative to A. Since C is south west of B, we can subtract 1 from both the X and Y co-ordinates of B.

C is assigned the co-ordinates of (-1,-2)

And finally, with the last rule C N A, we have seen both points before and have already generated co-ordinates for both. 

We can therefore validate whether the direction N, conforms to the positioning of both co-ordinates. In this case, the C co-ordinates are definitely south of A, and therefore this rule is invalid.